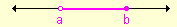x²+4x+2 ≤ - 3
Solución:
x²-3x+3 ≤ 0
Factorizando
( x+3 ) ( x+1 )
√x²=x
Sum Mul
4 3
3 1
Luego
(x+3)(x+1) ≤ 0
Caso 1
Se pide
x+3 ≥ 0 y x+1 ≤ 0
x ≥ -3 y x ≤ -1

x ∈ [-3, -1]
Caso 2
Se pide
x+3 ≤ 0 y x+1 ≥ 0
Resolviendo las desigualdades
x < --3 y x ≥ -1

x ∈ ᴓ
Su solucion
x ∈ [-3, -1] U ᴓ
x ∈ [-3, -1]